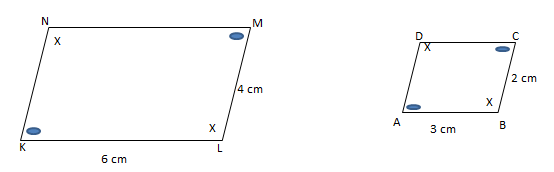
Postingan ini membahas contoh soal bangun datar yang sebangun dan kongruen yang disertai pembahasannya. Dua bangun datar di atas adalah dua bangun yang sebangun dengan memiliki beberapa sifat seperti yang ada di bawah ini.
Kesebangunan Dan Kekongruenan Bangun Datar Alan Bagus
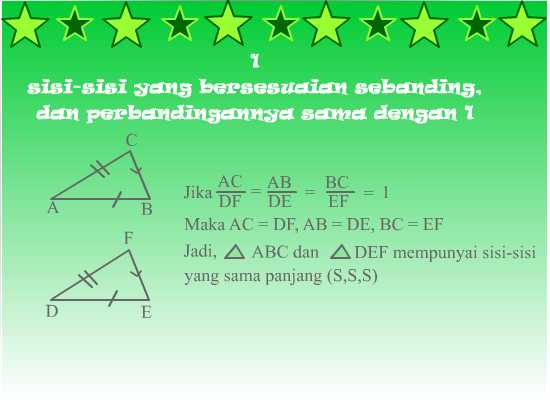
Contoh bangun datar yang sebangun. Pasangan sisi sisinya yang bersesuaian mempunyai perbandingan nilai yang sama. Kalian diharapkan dapat mengidentifikasi bangun bangun datar yang sebangun dan kongruen sifat sifat dua segitiga sebangun dan kongruen. Oleh karena dua bangun dikatakan sebangun apabila sisi sisi yang bersesuaian mempunyai perbandingan yang senilai maka kita dapat menghitung panjang salah satu sisi yang belum diketahui dengan menggunakan konsep perbandingan seperti pada contoh berikut ini. Terdapat macam macam bangun datar diataranya persegi panjang persegi segitiga jararan. Pada akhirnya kalian dapat menggunakan konsep kesebangunan ini dalam memecahkan masalah sehari hari. Kita dapat menggunakan sifat dari dua bangun datar yang sebangun.
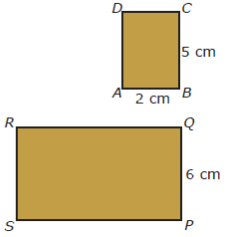
Kita dapat menggunakan sifat dari dua bangun datar yang sebangun. Bangun datar dikatakan kongruen jika memenuhi syarat yaitu memiliki ukuran ukuran sisi yang bersesuaian yang sama dan memiliki ukuran ukuran sudut yang bersesuaian yang sama. Bangun datar pengertian macam macam jenis bangun datar sifat sifat bangun datar dan rumus bangun datar serta contoh soal bangun datar terlengkap bangun datar adalah sebutan untuk bangun bangun dua dimensi gabungan bangun datar dapat membentuk bangun ruang seperti tabung atau yang lainnya. Tentukan nilai x dan y. Tentukan nilai x dan y. Diketahui dua bangun datar di bawah sebangun.
Diketahui dua bangun datar di bawah sebangun. Tentang kesebangunan dan kekongruenan yang meliputi tentang pengertian dan contoh contohnya. Dari keempat pasangan bangun datar pada opsi jawaban yang pasti sebangun adalah dua buah persegi karena pajang sisi persegi sama besar di semua sisi. Karena memiliki empat sisi yang sama panjang otomatis dua bangun persegi akan bersifat kongruen karena perbandingan sisi sisi yang bersesuaian akan selalu sama begituula besar sudutnya. Yaitu perbandingan panjang sisi yang bersesuaian senilai untuk menghitung panjang salah satu sisi yang belum diketahui dari dua bangun yang sebangun. Yaitu perbandingan panjang sisi yang bersesuaian senilai untuk menghitung panjang salah satu sisi yang belum diketahui dari dua bangun yang sebangun.
Kesebangunan dan kekongruenan bangun datar segitiga dan trapesium hallo sahabat pada bab kali ini kita akan membahas materi yang sering muncul dalam kisi kisi ujian nasional yaitu.