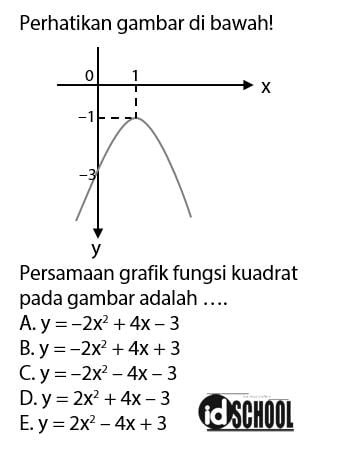
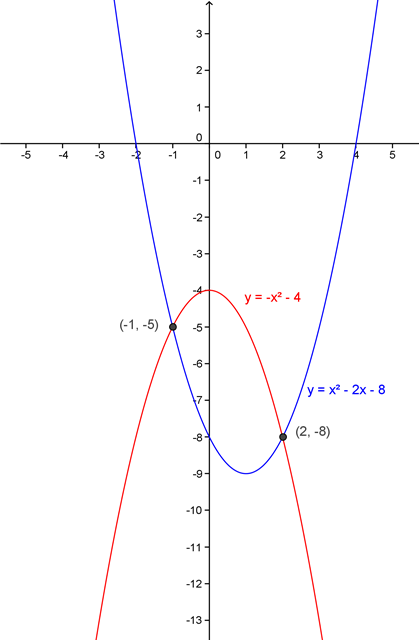
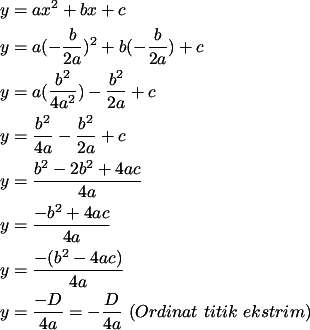Biasanya pertanyaan berkutat tentang nilai ekstrem titik puncak bagaiman gambar grafiknya sumbu simetri dan lain lain. Di sma sering sobat jumpai soal tentang grafik fungsi kuadrat.
Fungsi Kuadrat Grafik Rumus Menyusun Persamaan Contoh Soal
Contoh soal fungsi kuadrat dan grafik parabola. Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y. Titik potong dengan sumbu x. Bentuk umum fungsi kuadrat. Untuk memastikan bahwa persamaan kuadrat di atas mempunyai akar maka langkah pertama adalah menentukan terlebih dahulu diskriminannya. Grafik fungsi kuadat ini gambarnya berbentuk parabola. Untuk menggambarnya diperlukan langkah langkah sebagai berikut.
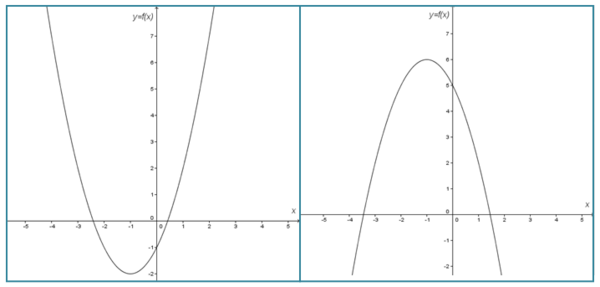
Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola. Mari kita bedah bersama fungsi kuadrat dari fxx 2 6x8. ƒx ɑx 2 bx c a b dan c r ɑ 0 untuk semua nilai x dalam daerah asalnya. Sebagai contoh grafik dari fungsi. Fungsi kuadrat juga dikenal sebagai fungsi polinom atau fungsi suku banyak berderajat dua dalam variabel x. Bentuk umum fungsi kuadrat adalah fx ax 2 bx c 0 dimana a b dan c adalah bilangan real dan a 0.
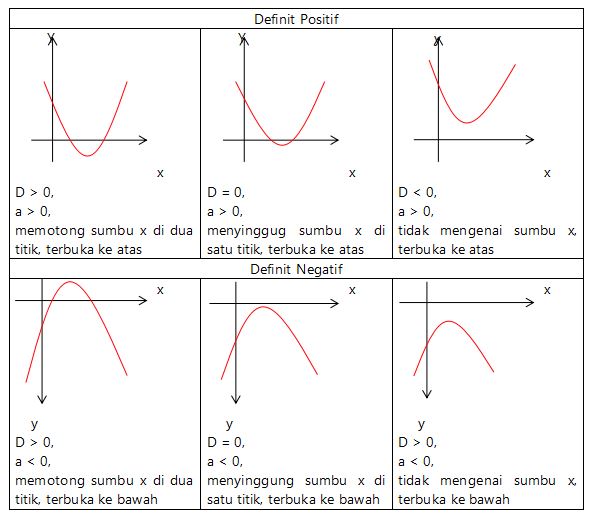
1 menentukan titik potong dengan sumbu x syaratnya y 0 sehingga ax 2 bx c 0 x x 1 x x 2 0. Untuk menggambar grafik fungsi kuadrat maka rumus yang kita perlukan adalah rumus untuk menentukan sumbu simetri parabola rumus menentukan nilai ekstrim dan titik balik dan tentu saja cara menentukan titik potong terhadap sumbu x dan sumbu y. Yang namanya grafik fungsi kuadrat adalah grafik dengan bentuk parabola seperti gunung atau lembah. Ingat titik potong dengan sumbu x akan didapatkan apabila nilai y0 maka dari itu akan didapatkan bentuk persamaan kuadrat x 2 6x80. Bentuk dan karakteristik dari suatu grafik fungsi kuadrat sangat bergantung pada nilai kontstanta a. Kemudian pasangan nilai x y tersebut menjadi koordinat dari yang dilewati suatu grafik.
Grafik fungsi kuadrat dalam bidang cartesius dikenal sebagai parabola.
Gallery of Contoh Soal Fungsi Kuadrat Dan Grafik Parabola
