Nilai maksimum dan minimum yang dimaksud untuk suatu fungsi adalah nilai maksimum dan minimum lokal artinya hanya berlaku pada interval tertentu saja. Nilai maksimum dan minimum yang dimaksud untuk suatu fungsi adalah nilai maksimum dan minimum lokal artinya hanya berlaku pada interval tertentu saja.

Nilai Optimum Suatu Fungsi Objektif Program Linear Fungsi
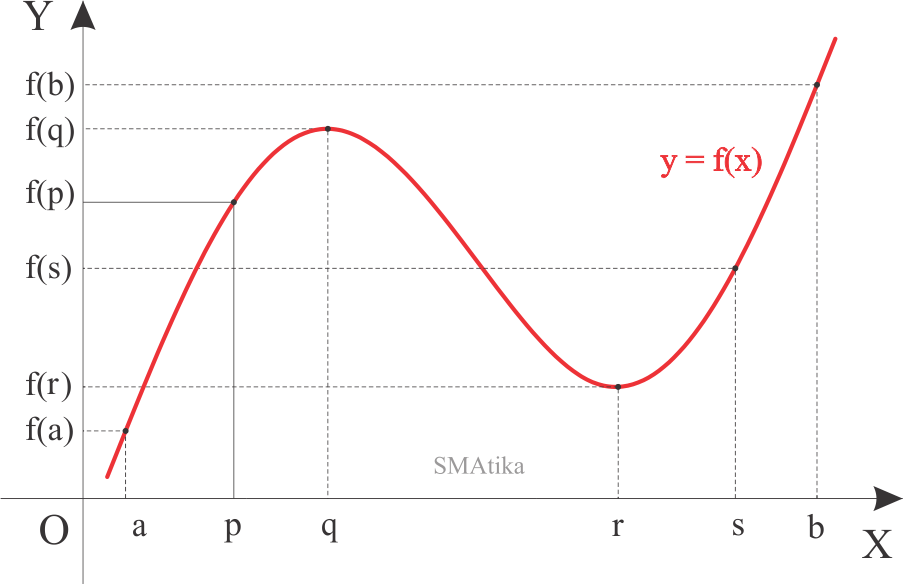
Contoh soal nilai maksimum dan minimum. Dan dinamakan titik minimum mutlak dari fungsi pada selang 𝐼. Buku matematika gulam halim 13177 views. Jika f berubah tanda dari positif ke negatif maka f c merupakan nilai maksimum lokal. Tentukan nilai maksimum a y 3 sin 2x5 b y 2 cos 3x98 o 7 c y 4 cos 4x frac pi2 3. Pada postingan ini kita akan membahas penyelesaian contoh soal nilai stasioner nilai minimum dan nilai maksimum. Dan dinamakan titik maksimum lokal dari fungsi pada selang 𝐼.
Sedangkan yang dimaksud dengan interval tertutup adalah interval dengan batas yang termasuk dalam interior point. Misalkan c adalah bilangan kritis fungsi kontinu f dan f terturunkan pada setiap titik pada interval yang memuat c kecuali mungkin di cbergerak melewati c dari kiri ke kanan. Untuk menentukan nilai minimum atau maksimum fungsi fx dalam interval tertutup terlebih dahulu ditentukan nilai fx untuk nilai x sebagai titik ujung interval domain fungsi fx dan nilai x yang menyebabkan f x 0. Nilai balik minimum fc bukan merupakan nilai minimum fungsi fx akan tetapi dinamakan nilai minimum lokal atau minimum relatif. Misalkan 2 bagian sudut adalah x dan α x maka fxcosx cosα x. Kumpulan pembahasan soal unbk.
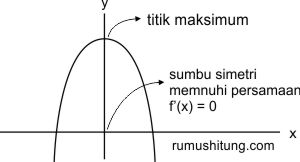
642 fungsi kuadrat nilai maksimum dan minimum. Setelah anda memahami bagaimana cara menentukan nilai maksimum dan minimum fungsi trigonometrisekarang kita lihat aplikasinya dalam beberapa contoh soal. Fungsi dikatakan mencapai maksimum lokal di jika terdapat suatu 𝛿 0 sehingga pada selang 𝛿 𝛿 berlaku di sini dinamakan nilai maksimum lokal. Nilai maksimum minimum pada interval contoh 1 duration. Nilai maksimum dan nilai minimum suatu fungsi dalam hal ini kurang lebih dapat diartikan nilai yang terbesar dan terkecil fungsi tersebut dalam interval tertutup tertentu. Bagilah sudut lancip α menjadi 2 bagian sehingga hasil perkalian kosinus kosinusnya mencapai nilai maksimum.
Tentukan nilai maksimum itu. Menghitung nilai maksimum atau minimum yang diminta dengan substitusi nilai variabelnya ke fungsi awal. Jika suatu fungsi fx mempunyai turunan fx 0 0 maka nilai fx 0 disebut sebagai nilai stasioner dan x 0 fx 0 disebut titik stasioner. Titik minimum diawali oleh grafik turun kemudian naik. Menghitung nilai maksimum atau minimum yang diminta dengan substitusi nilai variabelnya ke fungsi awal. Jika f berubah tanda dari negatif ke positif maka f c merupakan nilai minimum lokal.